Teoría de cartera de markowitz

A grandes rasgos se define una cartera de inversiones como un conjunto de activos en donde tenemos invertido nuestro dinero de forma diversificada, dependiendo de la naturaleza de estos activos pueden ser de renta fija o renta variable. En la realidad naturalmente encontramos carteras mixtas, las cuales se componen de estos dos tipos de activos nombrados anteriormente. 

Entrando de lleno al modelo de Markowitz podemos decir que marcó un antes y un después a la hora de elegir una inversión o no, ya que antes de 1952 la mayoría de los inversionistas se concentraban netamente en la maximización de la rentabilidad de sus acciones, en otras palabras, buscaban la inversión que mayores ganancias podría generarles.

Aquí es donde entra Harry Markowitz planteando que el riesgo que tiene cada activo es sumamente importante a la hora de tomar una decisión de inversión, para 1952 publica un artículo en el journal of finance llamado portfolio selection, en donde expone que se debe tener en cuenta la importancia del riesgo a la par de las rentabilidades, también hace énfasis en que la diversificación puede reducir el efecto del riesgo. Esto basado en la idea de que por mucha rentabilidad que pueda generar un activo o conjunto de estos, si la probabilidad de perder una gran parte o incluso todo nuestro dinero ¿Qué sentido tiene que la rentabilidad esperada sea muy elevada?

La teoría de formación de cartera de inversión se compone de tres principales etapas: 

• Determinación del conjunto de carteras eficientes.
• Determinación de la actitud de inversor frente al riesgo.
• Determinar la cartera optima. 

Aparte de estas etapas el autor apoya la teoría con los siguientes supuestos:

1.  La rentabilidad de una cartera viene dada por su esperanza matemática o media.
2. El riesgo de una cartera se mide a través de la volatilidad (según la varianza o desviación típica).
3. El inversor siempre prefiere la cartera con mayor rentabilidad y menor riesgo. Ver relación rentabilidad, riesgo y liquidez.

Con determinar el conjunto de carteras eficientes 

Observando el método de una forma general podemos decir que, una cartera eficiente aquella que ofrece el mínimo riesgo para un valor de rentabilidad esperado.

 

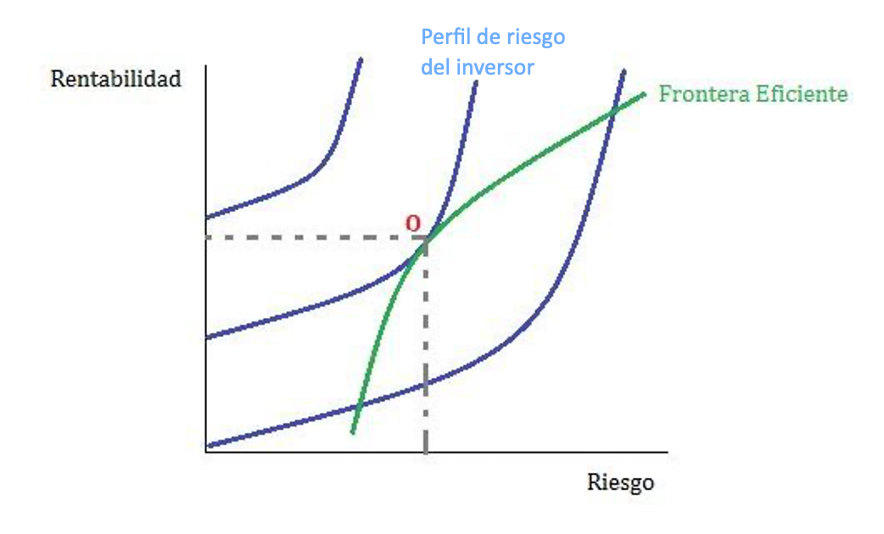
Como se ve en la gráfica, en la frontera de cartera eficiente, cada de estas carteras minimiza el riego de una rentabilidad dada. Para aumentar la rentabilidad debemos asumir un aumento del riego. 

La frontera eficiente la encontramos maximizando los rendimientos, sujeto a algunas restricciones como:

• Restricción paramétrica 
• Restricción presupuestaria 
• Condición de no negatividad 

Determinación de la actitud del inversor frente al riego

La actitud del inversor frente al riesgo se determina con su mapa de curvas de indiferencia, esto es un conjunto de curvas que representan las preferencias de este mismo. 

Cuanto más arriba se encuentre la curva, mayor satisfacción le entregara al inversor.

 

 

Por último, la determinación de la cartera optima está dada en el punto de equilibrio “0” en donde se interceptan la curva de la frontera eficiente y una de las curvas de indiferencias del inversor (perfil de riego), como se puede apreciar en la imagen anterior.

Las curvas que estén por debajo de este punto darán menos satisfacción y las que estén por encima no serán factibles.

publicado por Bastian Calbuñir